네이버 블로그로 이전했습니다.
https://blog.naver.com/moongda0404/222729519749
[Python Data Analysis 분석 6] 데이터 분석 - 파이썬 선형 회귀분석(1/2)
*본 글은 Python3을 이용한 데이터 분석(Data Analysis)을 위한 글입니다. 회귀분석의 사전적 의미는 &q...
blog.naver.com
*본 글은 Python3을 이용한 데이터 분석(Data Analysis)을 위한 글입니다.
회귀분석의 사전적 의미는 "관찰된 연속형 변수들에 대해 두 변수 사이의 모형을 구한 뒤, 적합도를 측정해 내는 분석 방법이다"라고 적혀있습니다.
이외에도 '회귀'는 '돌아오다'라는 의미가 있습니다. 결과를 바탕으로 관계를 역으로 찾아서 거슬러 올라가는 느낌이라 회귀라고 부르는 것은 아닌가 합니다.
밑에 보시면 하나의 그래프가 있습니다.
선 주위에는 빨간 점들이 있는데, 이 점들을 이용해 파란 선의 함수를 예측하는 것이 회귀 분석입니다.
즉 회귀분석은 빨간 점들이 가지는 좌표 데이터를 기반으로 y=ax를 구하고, 향후 다른 빨간 점들이 어디에 위치할 것인지를 예측할 수 있는 분석 방법입니다.
이 글에서는 야구선수 데이터를 통해 회귀 분석을 연습해보겠습니다.
목표 : 어떤 속성이 연봉에 영향을 끼치는지 분석하고, 2017년 데이터를 학습하여 2018년 연봉을 예측하기.
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import warnings
warnings.filterwarnings("ignore")
picher_file_path = '../data/picher_stats_2017.csv'
picher = pd.read_csv(picher_file_path)데이터를 읽습니다. warnings는 경고메시지를 무시하기 위해 사용했는데, 없어도 무방합니다.
그럼 데이터의 형식을 살펴보겠습니다.
|
picher.head()
|

각 선수별 경기 정보와 승률, 연봉이 적혀있습니다.
칼럼도 살펴보겠습니다.
|
picher.columns
|

그럼 여기서 우리는 y는 무엇인지, x는 무엇인지 알 수 있습니다.
y=연봉(2018)
x=그 외
어떤 x가 중요한지 찾는 과정을 진행하겠습니다.
우선 각 칼럼명이 한글이기에, 한글폰트로 설정하여 에러를 방지하겠습니다.
저는 '바탕'이 익숙하여 바탕으로 선택했습니다.
import matplotlib as mpl
# 현재 OS 내에 설치된 폰트를 확인합니다.
set(sorted([f.name for f in mpl.font_manager.fontManager.ttflist]))
|
mpl.rc('font', family='Batang')
|
예측 대상인 연봉에 대한 정보를 보겠습니다.
|
picher['연봉(2018)'].hist(bins=100)
|
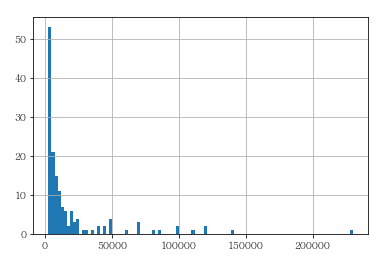
주로 분포는 5억이하로 분포하고 있는데, 몇몇 고연봉 선수가 있기도 합니다.
이를 다른 형식으로도 봐보겠습니다.
|
picher.boxplot(column=['연봉(2018)'])
|
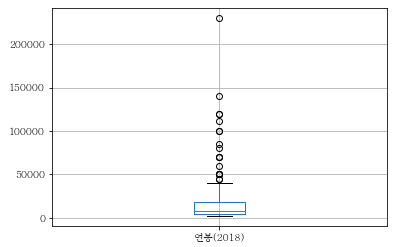
평균 박스권은 아래에 위치하지만 몇몇 값이 확 위로 튀는 걸 알 수 있네요.
어떤 특징이 저런 차이를 내는지 알아보고, 모델링한다면 괜찮은 예측 모델을 만들 수 있을 겁니다.
.
.
.
제일 먼저 할 일은, 단위를 통일하는 것입니다.

현재 테이블은 각 특징(x)의 자릿수가 서로 다르기에, scaling작업을 통해 같은 범위로 압축시켜야 합니다.
# 피처 각각에 대한 scaling을 수행하는 함수를 정의합니다.
def standard_scaling(df, scale_columns):
for col in scale_columns:
series_mean = df[col].mean()
series_std = df[col].std()
df[col] = df[col].apply(lambda x: (x-series_mean)/series_std)
return df컨셉은 '각각의 평균을 표준편차로 나눈 값은 수렴한다'라고 생각됩니다.
확률과 통계에서 자주 나오는 표준편차와 분산은 보통 -1~+1 사이에서 분포한다는 점과 연관하여 생각해보았습니다.
그럼 scailing 결과를 보겠습니다.
# 피처 각각에 대한 scaling을 수행합니다.
scale_columns = ['승', '패', '세', '홀드', '블론', '경기', '선발', '이닝', '삼진/9',
'볼넷/9', '홈런/9', 'BABIP', 'LOB%', 'ERA', 'RA9-WAR', 'FIP', 'kFIP', 'WAR', '연봉(2017)']
picher_df = standard_scaling(picher, scale_columns)
picher_df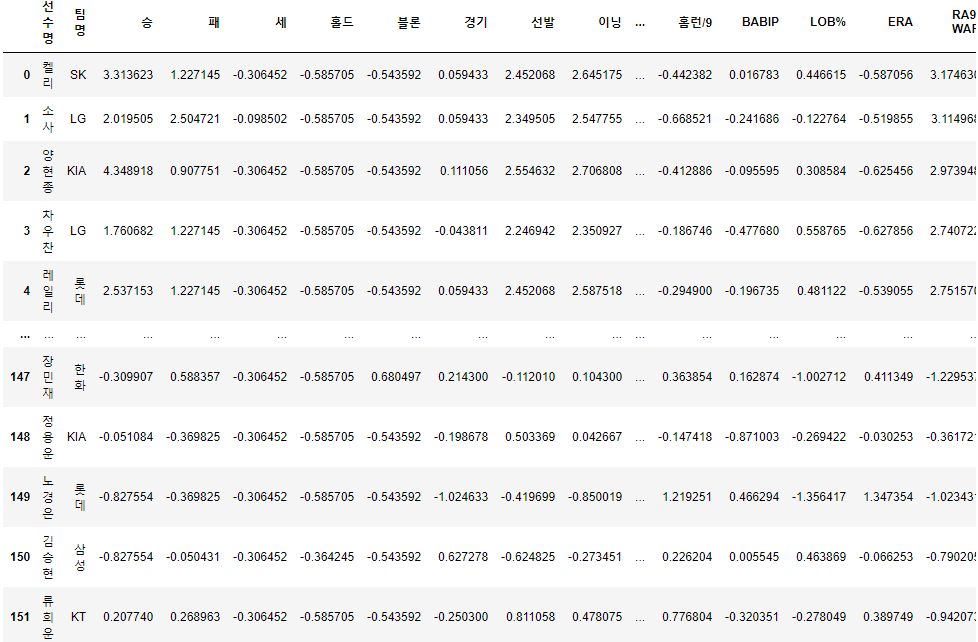
각 칼럼들이(x들) 한자리 단위로 수렴하게 바뀌었습니다. 이제 각 특징들을 함께 묶어 비교해도 큰 문제가 없을 겁니다.
잠시 다음 단계로 넘어가기 전, y를 명확히 표시하기 위해 칼럼 : '연봉(2018)'의 이름을 'y'로 변경하겠습니다.
picher_df=picher_df.rename(columns={'연봉(2018)' : 'y'})
picher_df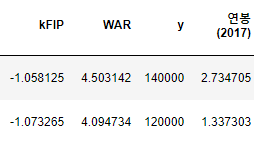
다음 단계는 숫자가 아닌 값들을 숫자로 전처리하는 과정을 진행합니다.
테이블을 보시면 현재 선수명과 팀명이 숫자 값이 아닌데, 변경이 필요합니다.
1. 선수명 : 선수의 이름은 연봉에 영향을 끼치지 않을 것이므로 삭제
|
picher_df = picher_df.drop('선수명', axis=1)
|
2. 팀명 : 해당 행(row)이 어떤 팀이냐를 0 or 1로 구분
각 선수가 어떤 팀인지 0과 1로 표현하기 위해선 pd.get_dummies() 함수를 사용합니다.
team_encoding = pd.get_dummies(picher_df['팀명'])
#더미로 만든 뒤 '팀명'은 필요가 없어졌으니 삭제
picher_df = picher_df.drop('팀명', axis=1)
team_encoding해당 팀 = 1
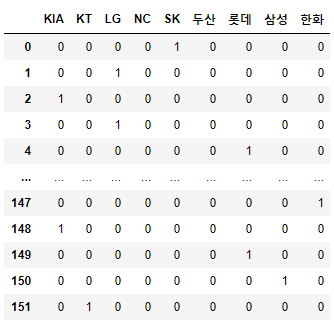
그럼 이 데이터를 picher_df에 붙입니다.
picher_df = picher_df.join(team_encoding)
picher_df
현재 picher_df는 152개의 데이터를 가지고 있습니다.
여기서 회귀분석을 위해 두 가지로 나누어야 하는데, [학습 데이터]와 [검증 데이터]로 나누어야 합니다.
학습데이터 : 모형 추정 즉, 학습을 위한 데이터.
검증데이터 : 성능 검증을 위한 데이터.
왜 멀쩡한 테이블을 두 가지로 나누는 걸까요?
→이유는 교차검증을 위해서입니다.
예측모델이 잘 만들어졌는지 보려면 알고 있는 정답과 비교를 해봐야 합니다. 그래서 보통 80%의 데이터만으로 학습을 하고, 나머지 20%는 학습한 모형이 잘 작동하는지 확인하기 위한 검증 데이터로 뺍니다.
그럼 학습을 진행해보겠습니다.
from sklearn import linear_model
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_squared_error
from math import sqrt
# 학습 데이터와 테스트 데이터로 분리합니다.
#'선수명', 'y'를 제외한 칼럼들은 X
X = picher_df[picher_df.columns.difference(['선수명', 'y'])]
y = picher_df['y']
#검증(test)는 20%로 한다. = test_size=0.2
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=19)여기서 random_state는 난수를 발생시키는 것인데, 20%의 검증 데이터를 변형시켜서 학습을 진행할 때 '과적합'에 빠지지 않도록 도와주는 역할을 합니다.
과적합 : 학습 데이터 대상 적중률은 100%에 가깝지만 새로운 외부 데이터는 적중률이 현저히 낮은 현상
이제 회귀 분석 계수를 학습하고 출력해봅니다.
# 회귀 분석 객체 생성(선형 회귀 모델 생성)
lr = linear_model.LinearRegression()
#fit()는 기울기와 절편을 전달하기 위함.
model = lr.fit(X_train, y_train)
# 학습된 계수를 출력합니다.
print(lr.coef_)
# 상수항을 출력합니다.
print(lr.intercept_)
해당 계수들을 보면, '51584.44818152'가 가장 영향도가 높다고 나옵니다.
그럼 완성한 모델을 이용해 새로운 값을 가지고 예측을 해봅니다.
#새로운 데이터x에 대한 y결과를 예측할 수 있다.
y_predicted=model.predict(x_predicted)
여기선 새로운 값을 가지고 오기 귀찮으니 test용으로 썼던 'X_test'를 사용하겠습니다.
x_new=X_test
y_new=model.predict(x_new)여기서 y_new가 각각의 x_new에 대한 2018년 연봉을 예측했을 겁니다.
|
print(type(y_test))
|
타입이 Series네요. DataFrame으로 고쳐서 실제 y_test와 비교를 해보겠습니다.
y_compare={'y_test':y_test, 'y_predicted':y_new}
pd.DataFrame(y_compare)
일부 확인해보니 3번째 행이나 4번째 행은 거의 유사하고, 2번째 행은 오히려 마이너스가 나옵니다.
뭔가 맞는듯하면서도 어떤 값들이 방해를 하는 것 같군요.
하지만 꽤 많은 값이 들어맞았습니다!
차트로 한 번 보겠습니다.
mpl.rc('font', family='Batang')
y_compare.plot(y=['y_test', 'y_predicted'], kind="bar")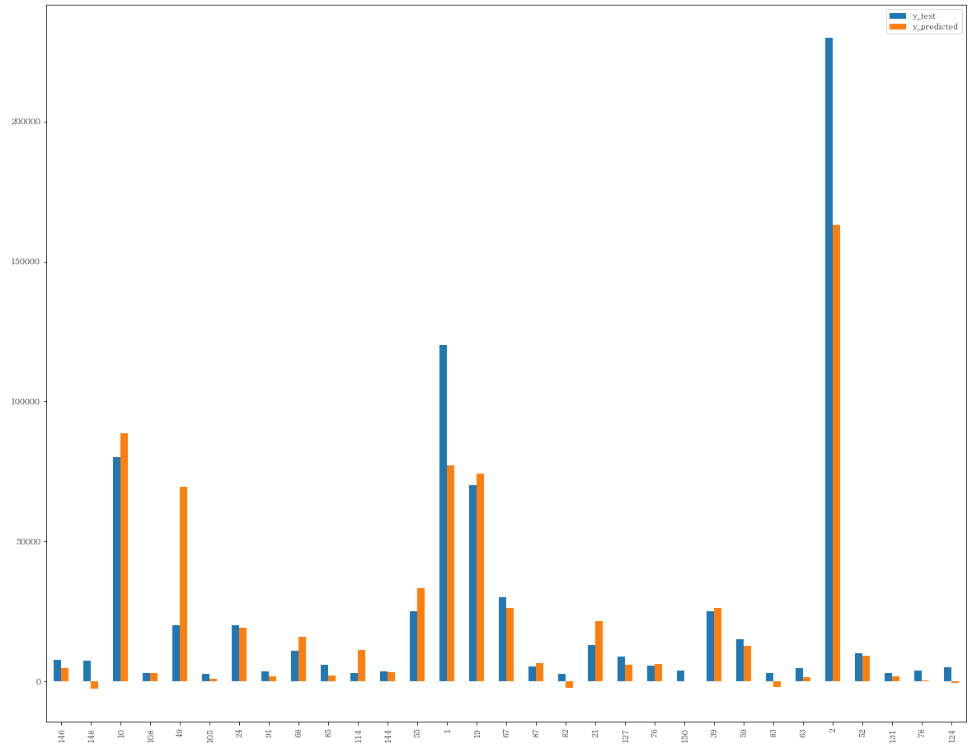
파란색이 실제값이고 주황색이 예측값인데, 상당히 유사한 모양을 보이네요
다음 시간에는 마이너스가 나올 수 있는 요소들을 제거하고, 특징을 간추려 정확성을 높이는 모델 평가 단계를 진행하겠습니다.
'데이터 분석 기초 > 분석 기법' 카테고리의 다른 글
| [Python Data Analysis 분석 8] 데이터 분석 - 파이썬 시계열분석 (6) | 2020.06.24 |
|---|---|
| [Python Data Analysis 분석 7] 데이터 분석 - 파이썬 선형 회귀분석(2/2) (1) | 2020.06.16 |
| [Python Data Analysis 분석 5] 데이터 분석 - 파이썬 연관관계 분석(음식 메뉴) (4) | 2020.06.11 |
| [Python Data Analysis 분석 4] 데이터 분석 - 파이썬 상관관계 분석(타이타닉) (1) | 2020.06.09 |
| [Python Data Analysis 분석 3] 데이터 분석 - 식당 데이터 분석해보기(3/3) (2) | 2020.06.08 |




댓글