네이버 블로그로 이전했습니다.
https://blog.naver.com/moongda0404/222729524245
[Python Data Analysis 분석 7] 데이터 분석 - 파이썬 선형 회귀분석(2/2)
*본 글은 Python3을 이용한 데이터 분석(Data Analysis)을 위한 글입니다. 지난 글에 이어, 회귀 분석 ...
blog.naver.com
*본 글은 Python3을 이용한 데이터 분석(Data Analysis)을 위한 글입니다.
지난 글에 이어, 회귀 분석 모델을 평가하고 성능을 높여보겠습니다.
우선 예측 모델이 어느정도 성능인지 보고 싶네요.
여기서는 R2 Score 와 RMSE Score를 이용하겠습니다.
R2 Score(결정계수) : 실제값, 예측값, 평균값 사이의 편차를 점수로 매긴 것
(값이 1에 가까울 수록 100%, 0에 가까울 수록 0%)

RMSE Score(평균제곱근 오차) : Root Mean Square Error.
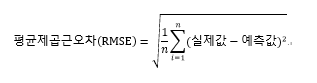
print(model.score(X_train, y_train)) # train R2 score를 출력합니다.
print(model.score(X_test, y_test)) # test R2 score를 출력합니다.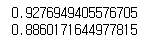
1에 가까울 수록 좋은거니까, 꽤 괜찮은것 같습니다.
R2 =0.7 → 70%의 예측 정확성
y_predictions = lr.predict(X_train)
print(sqrt(mean_squared_error(y_train, y_predictions))) # train RMSE score를 출력합니다.
y_predictions = lr.predict(X_test)
print(sqrt(mean_squared_error(y_test, y_predictions))) # test RMSE score를 출력합니다.
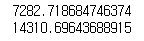
둘의 차이를 찾아봤는데, RMSE는 데이터의 크기에 따라 천차만별의 SCORE가 나오기에 판단하기에 어려움이 있다고 합니다. 보통은 R2의 성능평가를 신빙성있게 사용한다고 합니다.
.
.
.
그럼 성능을 끌어올린 뒤, 다시 R2를 진행하겠습니다.
다시 picher_df으로 돌아옵시다. (이 전 글에서 sklearn 학습에 사용한 dataframe)
|
picher_df
|
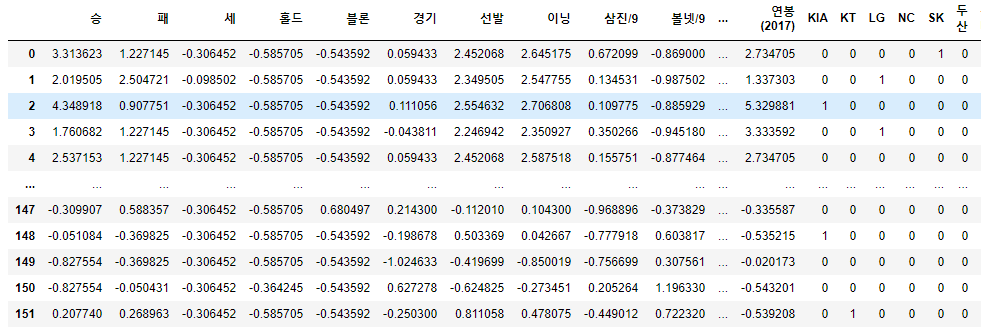
지난 글에서는 이 테이블을 통으로 회귀분석을 돌렸습니다.
대략적으로 유사한 예측이 가능하기는 했지만 전혀 엉뚱한 예측값이 나오기도 했습니다.
어떻게해야 성능을 높일 수 있을까요?
대표적인 방법으로 '다중공선성 제거'가 있습니다.
다중공선성 : 독립 변수간의 상관 관계가 강하게 나타나, 회귀분석에 악영향을 주는 경우
그럼 앞에서 언급했던 상관관계 분석을 통해 각 속성(독립변수) 사이의 상관 관계를 보겠습니다.
(팀명은 상관관계가 없음을 직관적으로 알 수 있으니, 제외하겠습니다.)
import seaborn as sb
picher_df_corr=picher_df[['승', '패', '세', '홀드', '블론', '경기', '선발', '이닝', '삼진/9', '볼넷/9', '홈런/9',
'BABIP', 'LOB%', 'ERA', 'RA9-WAR', 'FIP', 'kFIP', 'WAR', 'y',
'연봉(2017)']]
plt.rcParams['figure.figsize']=(15,10)
sb.heatmap(picher_df_corr.corr(),
annot=True,
cmap='Reds',
vmin = -1, vmax = 1
)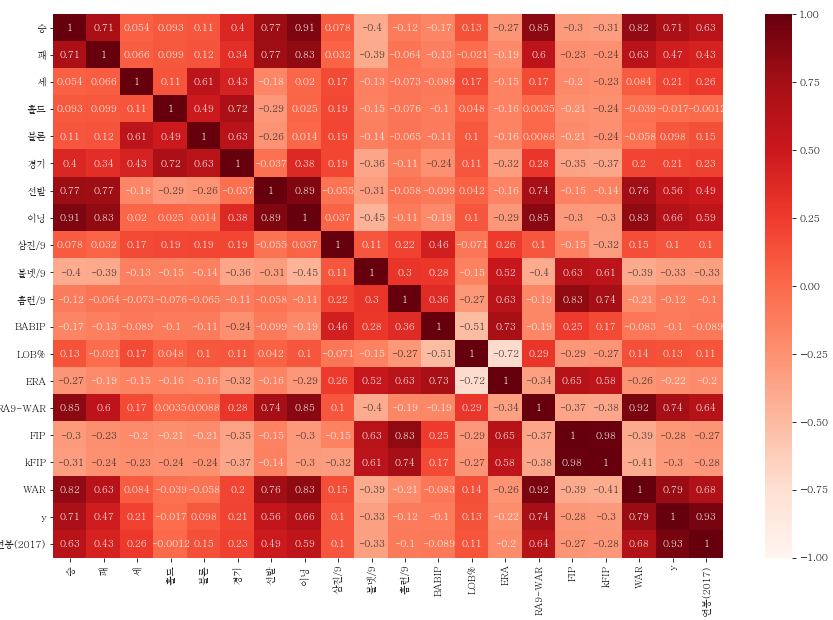
heatmap으로 보니 1, 혹은 -1에 가까운 상관계수값이 많이 보입니다.
상관관계가 강한 feature들이 가지고 있는 다중공선성이 어느정도인지를 확인해보겠습니다.
회귀 모델에서 다중공선성을 파악할 수 있는 대표적인 방법은 VIF입니다.
VIF (Variance inflation Factors 분산팽창요인)
안전 : VIF < 5
주의 : 5 < VIF < 10
위험 : 10 < VIF
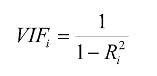
수식은 위와 같은데, 여기서는 바로 넘어가겠습니다.
VIF기능을 제공하는 라이브러리를 사용해 각 feature(독립변수)별 다중공선성 정도를 확인합니다.
from statsmodels.stats.outliers_influence import variance_inflation_factor
# 피처마다의 VIF 계수를 출력합니다.
vif = pd.DataFrame()
vif["VIF Factor"] = [variance_inflation_factor(picher_df_corr.values, i) for i in range(picher_df_corr.shape[1])]
vif["features"] = picher_df_corr.columns
vif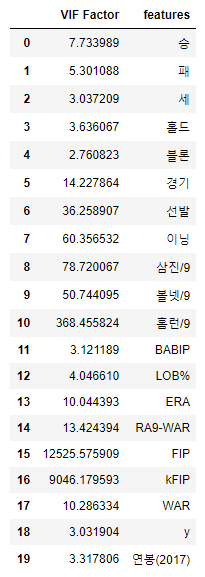
후보를 고른 뒤, 다시 회귀분석을 돌리겠습니다.
순서
1. VIF 계수가 높은 feature제거
2. 단 유사한 feature의 경우, 둘 중 1개만 제거(FIP, kFIP의 경우)
3. 제거 후 VIF계수 재출력
4. (1, 2, 3)의 과정 반복
5. 회귀분석 진행
6. feature의 p-value점검
위 순서를 차례대로 진행해보겠습니다.
1. VIF 계수 높은 feature 제거
picher_df_corr=picher_df_corr.drop(['홈런/9','kFIP',], axis=1)
vif = pd.DataFrame()
vif["VIF Factor"] = [variance_inflation_factor(picher_df_corr.values, i) for i in range(picher_df_corr.shape[1])]
vif["features"] = picher_df_corr.columns
vif
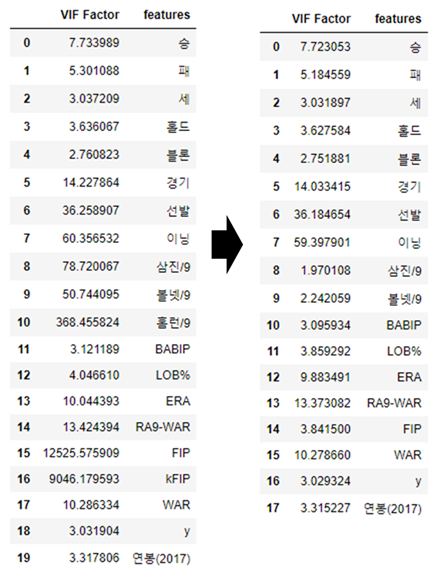
제거 후 VIF를 다시 측정해보니, 경기, 선발 등 일부 feature의 VIF수치가 낮아졌습니다.
이 중에서 VIF수치가 여전히 높은 feature들을 제거합니다.
picher_df_corr=picher_df_corr.drop(['선발','이닝'], axis=1)
vif = pd.DataFrame()
vif["VIF Factor"] = [variance_inflation_factor(picher_df_corr.values, i) for i in range(picher_df_corr.shape[1])]
vif["features"] = picher_df_corr.columns
vif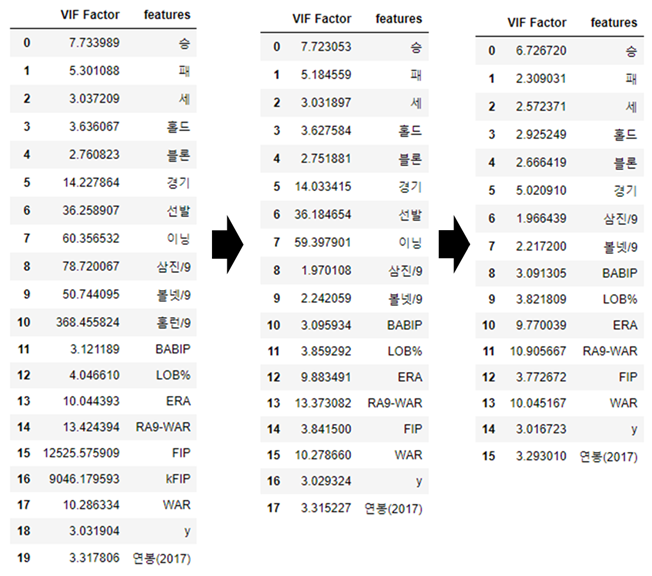
그럼 두번의 정제를 통해 얻은 feature들로 회귀분석을 진행합니다.
|
vif.features.values
|

위 명령어로 나온 feature들을 복사하면 좀 더 편하게 dataframe을 셋업할 수 있습니다.
회귀분석 진행
picher_df_corr_re=picher_df_corr[['승', '패', '세', '홀드', '블론', '경기', '삼진/9', '볼넷/9', 'BABIP', 'LOB%',
'ERA', 'RA9-WAR', 'FIP', 'WAR', 'y', '연봉(2017)']]
X=picher_df_corr_re[picher_df_corr_re.columns.difference(['y'])]
y=picher_df_corr_re['y']
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=19)
lr = linear_model.LinearRegression()
model = lr.fit(X_train, y_train)print(model.score(X_train, y_train))
print(model.score(X_test, y_test))
처음에 비해 둘 사이의 편차가 줄어든게 보이시나요?
선별한 feature가 효용성이 있으니, 여기서 좀 더 나아가보겠습니다.
이제 각 feature의 p-value를 확인합니다.
p-value는 해당 통계가 유의미한 가설인지 검증하는 수치입니다. (귀무가설 유의확률, 낮을수록 정확)
보통 0.05~0.01 이하면 유의미한 feature로 인정합니다.
import statsmodels.api as sm
X_train = sm.add_constant(X_train)
model = sm.OLS(y_train, X_train).fit()
model.summary()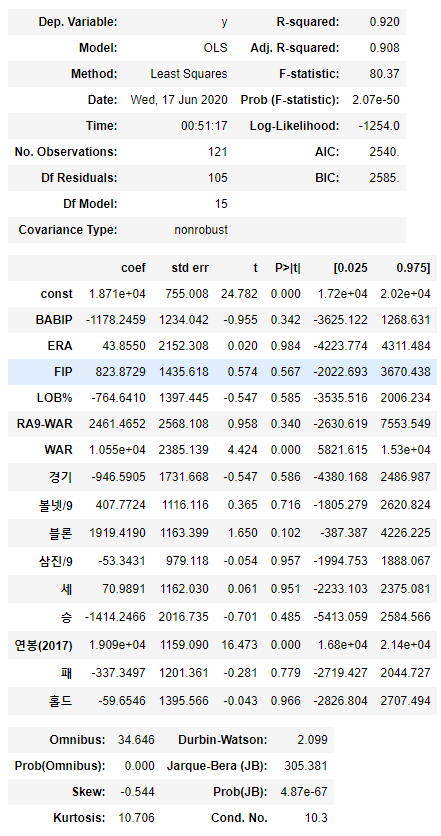
P>|t| 가 각 feature의 p-value입니다. 여기서는 실제 유의미한 값은 거의 없어서 최소값 순위로 추정해보겠습니다.
const는 상수이니 제외하고 'BABIP','RA9-WAR','블론','연봉(2017)' 을 사용했습니다.
picher_df_corr_re=picher_df_corr[['BABIP','RA9-WAR','블론','연봉(2017)','y']]
X=picher_df_corr_re[picher_df_corr_re.columns.difference(['y'])]
y=picher_df_corr_re['y']
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=19)
# 회귀 분석 객체 생성(선형 회귀 모델 생성)
lr = linear_model.LinearRegression()
#fit()는 기울기와 절편을 전달하기 위함.
model = lr.fit(X_train, y_train)
print(model.score(X_train, y_train))
print(model.score(X_test, y_test))
확실이 3번째에는 학습데이터와 테스트데이터의 편차가 미미하게 됐습니다. 이 말은, 서로 다른 데이터의 결과값이 유사하다는 의미입니다.
이제 마지막으로 선정한 feature가 얼마나 2018년 연봉을 잘 맞추는지 보겠습니다.
#최초의 csv 데이터 호출 : 실제 2018년 연봉값을 불러오기위함
temp_picher_df=pd.read_csv(picher_file_path)
X=picher_df[['BABIP','RA9-WAR','블론','연봉(2017)']]
predict_2018_salary = lr.predict(X)
picher_df['예측연봉(2018)'] = pd.Series(predict_2018_salary)
y_compare={'연봉(2018)':temp_picher_df['연봉(2018)'],'예측연봉(2018)':picher_df['예측연봉(2018)']}
y_compare=pd.DataFrame(y_compare)
y_compare_10 = y_compare.head(20)
mpl.rc('font', family='Batang')
y_compare_10.plot(y=['연봉(2018)', '예측연봉(2018)'], kind="bar")
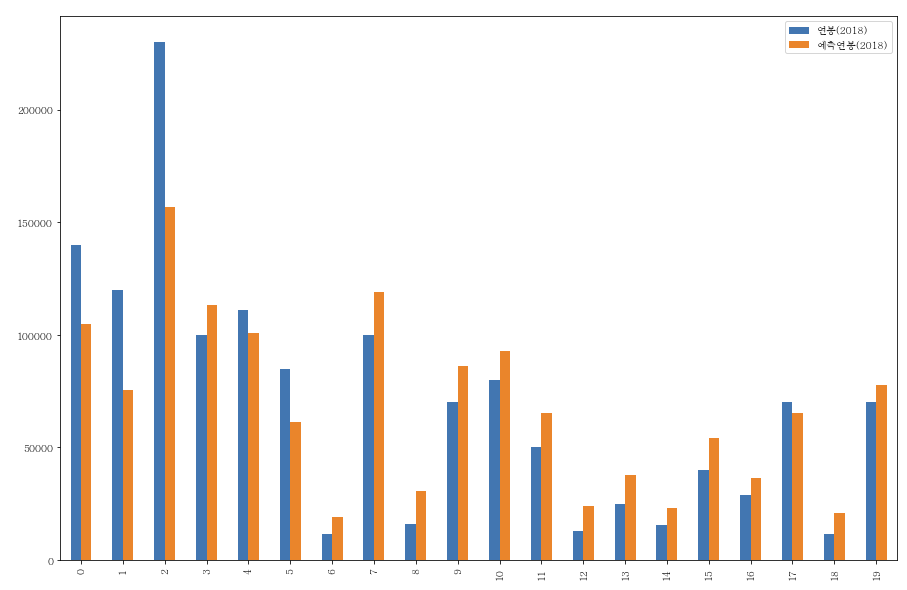
이 전 글에서 뽑았던 차트에 비해 적중률이 괜찮아보입니다. 예측연봉이 마이너스로 변하는 값도 보이지 않네요.
다음 글에서는 다른 예제를 통해 시계열 분석을 진행해보겠습니다.
'데이터 분석 기초 > 분석 기법' 카테고리의 다른 글
| [Python Data Analysis 분석 8] 데이터 분석 - 파이썬 시계열분석 (6) | 2020.06.24 |
|---|---|
| [Python Data Analysis 분석 6] 데이터 분석 - 파이썬 선형 회귀분석(1/2) (6) | 2020.06.16 |
| [Python Data Analysis 분석 5] 데이터 분석 - 파이썬 연관관계 분석(음식 메뉴) (4) | 2020.06.11 |
| [Python Data Analysis 분석 4] 데이터 분석 - 파이썬 상관관계 분석(타이타닉) (1) | 2020.06.09 |
| [Python Data Analysis 분석 3] 데이터 분석 - 식당 데이터 분석해보기(3/3) (2) | 2020.06.08 |




댓글